# 【基础算法】排序算法 (一)
对数组对象进行排序,获取” 有序 “数组对象。并非纯数字
# 前言说明
排序算法有八大,由简到难,每当别人问起来时,我却知其然不知其所然,我能看懂这个排序算法实现代码,但我应用起来却显得很艰难,最经典的是问过很多人冒泡排序怎么实现,他能讲的头头是道,但让他一写却频频出错,一问冒泡、选择、插入有什么区别就是懵逼数下的懵逼果,一百度一看就懂,过几个小时再问就对自己记忆力产生了怀疑。所以我想用自己的方式区分、总结、讲述八大排序算法,如有不懂欢迎评论。
# 名词解释
例子:数组 [4.2,2,6,4.1],比较的是整数部分,会发生 4.2 == 4.1 情况,请从小往大排序。
- 稳定排序:在稳定排序的算法结果下值为 [2,4.2,4.1,6],4.2 依旧在 4.1 前面。如 (冒泡排序,归并排序等)
- 非稳定排序:结果可能为 [2,4.1,4.2,6],如 (选择排序,希尔排序等)
- in-place: 占用常数内存,不占用额外内存,整体空间增加是 O (1),与数组长度 n 无关
- out-place: 占用额外内存,整体空间增加是 O (n),与数组长度 n 有关
# 循环比较排序
它们是选择排序,插入排序,冒泡排序,之所以叫循环比较排序是因为这类算法是将排序的数组视为一个整体,并对这个整体进行排序,实现上比较好理解都是两个循环外层循环数组确定无序与有序的分割位置,内层循环根据不同排序有小区别
- 选择:在无序数据中查找满足条件数据,属于拿着位置找数据。
- 插入:在有序数据查找可放置数据的位置,属于拿着数据找位置。
- 冒泡:从无序数据向分割位置” 载入 “满足条件数据,属于拿着位置找数据。
# 动图展示
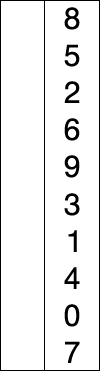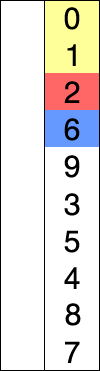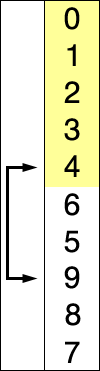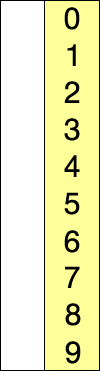
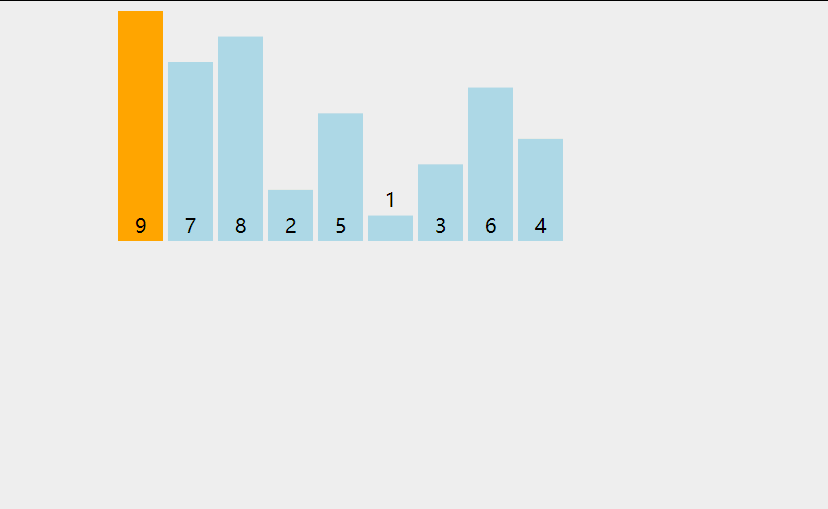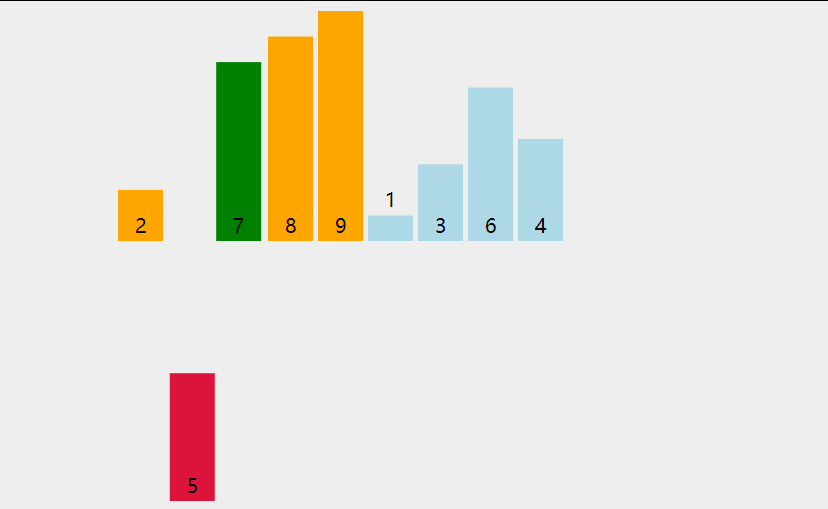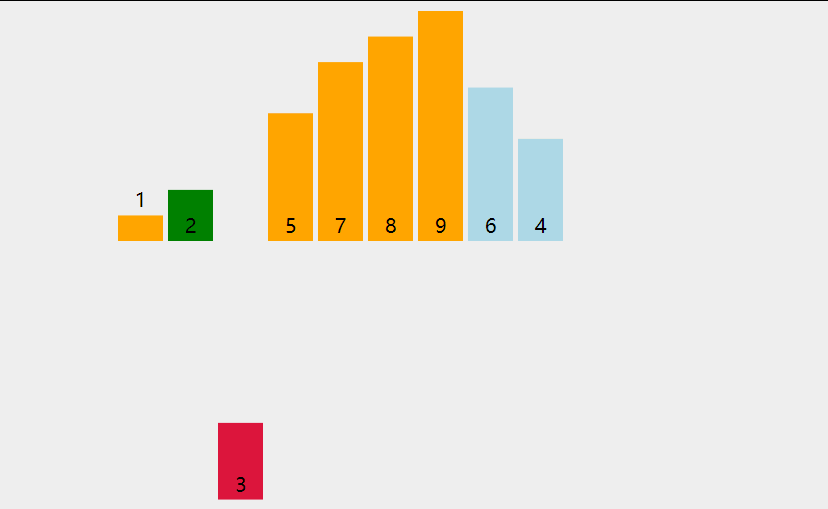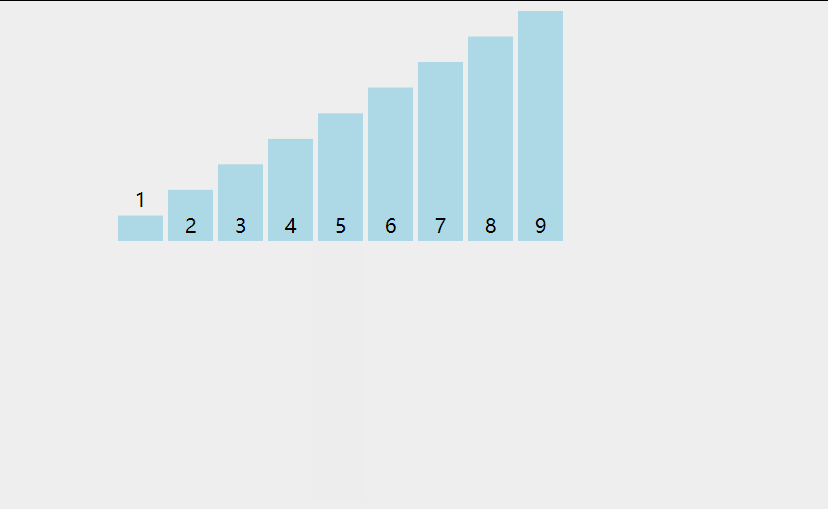
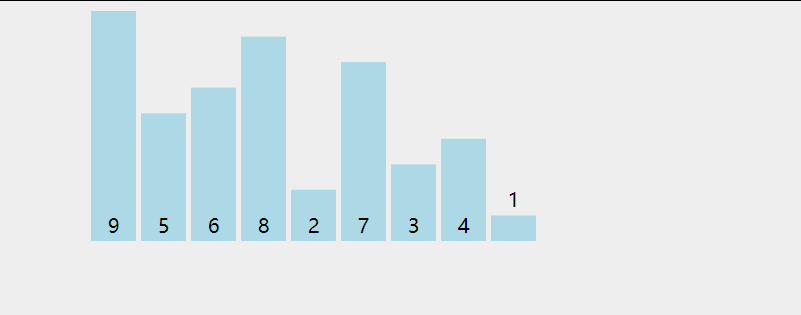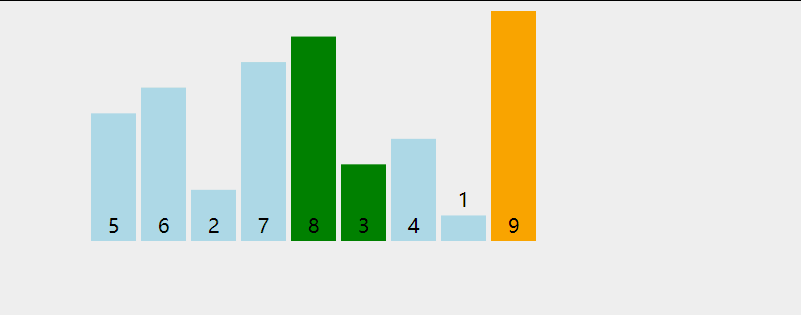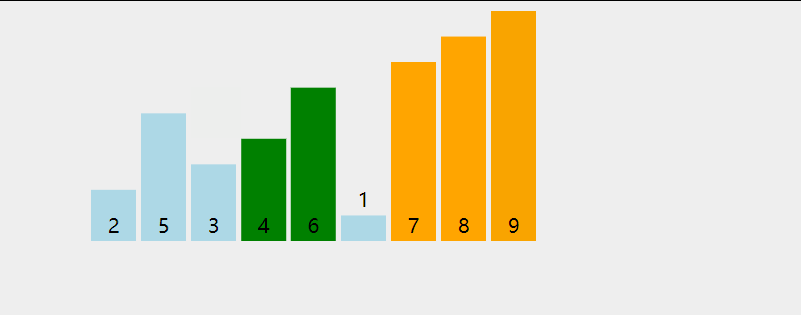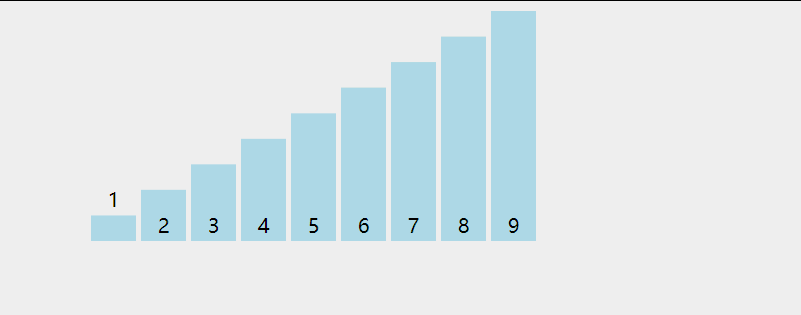
# 代码实现
下面三者代码实现差异在于:(为了方便理解下面,举例 [2,8,5,7,8,4],从小到大排序,循环位置是从数组左边往右进行)
- 选择:数据比较是从当前位置到最右边,在比较中定位最小数下标再和当前位置数据进行替换
- 插入:数据比较是从当前位置到最左边,在比较中定位比当前位置数据小的数下标并插入后面
- 冒泡:数据比较是从最右边到当前位置 (上面动图是从最左开始是反的),在比较不断替换两数位置确保小大排列直至当前位置数据
public class SelectSort { | |
public static int[] selectSort(int[] arr) { | |
// 数组长度小于 2 直接返回 | |
if(arr == null || arr.length < 2){ | |
return arr; | |
} | |
int n = arr.length; // 获取数组长度 | |
// 选择排序 | |
for (int i = 0; i < n - 1; i++) { // 从数组左向右循环 (最后一个数没有比较的意义,它已经经过替换是有序的) | |
int min = i; // 获取当前位置下标 | |
for (int j = i + 1; j < n; j++) { // 循环从当前位置后一位开始到数组最右边 (一定会循环至最后一位) | |
if (arr[min] > arr[j]) min = j; // 对比找到最小数的小标 (与下面直接交换位置导致算法不稳定原因) | |
} | |
// 交换位置 | |
int temp = arr[i]; | |
arr[i] = arr[min]; | |
arr[min] = temp; | |
} | |
// 插入排序 | |
for (int i = 0; i < n; i++) { // 从数组左向右循环 (到最后一个数) | |
int data = arr[i]; // 获取当前位置数据 | |
for (int j = i; j > 0; j--){ // 循环从当前位置往数组起点出发 (概率最好是第一次循环就条件满足) | |
if(data >= arr[j-1]){ // 因为从小往大排序,需确保数据放当前位置大于该位置前一个数 | |
arr[j] = data; // 条件满足,数据放当前位置 | |
break; // 退出本次循环 | |
} else { | |
arr[j] = arr[j-1]; // 条件不满足,当前位置前一个数移动到当前位置。(算法稳定原因) | |
} | |
} | |
} | |
// 冒泡排序 | |
for (int i = 0; i < n-1; i++) { // 从数组左向右循环 (最后一个数没有比较的意义,它已经经过替换是有序的) | |
boolean flag = true; // 判断是否有过位置交换 | |
for (int j = n-1; j > i; j--){ // 循环从最右边往当前位置点出发 (概率最好是第一次循环就条件满足) | |
if(arr[j] < arr[j-1]){ // 因为从小往大排序,需确保数据放当前位置大于该位置前一个数 | |
// 交换位置 (算法稳定原因) | |
int temp = arr[j]; | |
arr[j] = arr[j-1]; | |
arr[j-1] = temp; | |
flag = false; // 有过位置交换,就不能保证数据有序,需要继续循环,如 4 与 8 交换,但 8 还在 5 前面。 | |
} | |
} | |
if(flag){ // 没有过位置交换,退出循环。因为剩余数字每个数都大于它前一个数,所以才没有交换位置发生 | |
break; | |
} | |
} | |
return arr; | |
} | |
} |
# 思路差异
选择排序说到底是最像大家戏说的” 暴力破解 “,思路是将每个数都和非自身的其它数进行比较最后排出有序数组,冒泡排序的思路与选择排序的差异是它尽量利用了每次数之间比较时的信息,将数组进行调整使所有数字在位置上尽快接近正确位置,而插入排序的思路本质也与选择排序相同,但也是利用的是已排列好的数组这个信息,降低了无用的比较次数。
差异导致的结果,在最坏情况下无法看出,但在最好情况下非常明显,如传入一个 10 个数字的有序数组,选择排序要比较 90 次,冒泡排序 9 次,插入排序 9 次,因为选择排序无论如何要每个数都和非自身的其它数进行比较,所有时间复杂的还是 O (n^2),冒泡排序在第一轮外循环的 (n-1) 轮内循环发现一次位置都没交换,就能确保每个数与前面数都满足条件从而直接得出这个数组有序了,所以时间复杂度最好是 O (n),插入排序在 (n-1) 轮外循环的每次第一轮内循环发现当前数据与前面数据满足条件,直接找到这个数就在本位置,所有时间复杂度也是 O (n)。
# 总结
从以上分析和代码可以得出三种排序的相同点:最坏时间复杂度相同 O (n2),一般情况时间复杂度更趋向于 O (n2),空间复杂度是 O (1),原地排序 (in-place)。
它们三者之间的不同点
- 最好时间复杂度:选择 O (n^2),冒泡 O (n),插入 O (n)
- 稳定性:选择 (不稳定),冒泡 (稳定),插入 (稳定) // 在上面例子中选择排序会将两个 8 的位置互换所以不稳定
选择建议,大部分情况建议使用插入,理由如下。(不排除其它实际情况)
- 从理解难度上,我认为 选择 > 插入 > 冒泡
- 从单次循环代码量或者说赋值次数上 (cpu 每跑一个循环耗时) 选择 < 插入 < 冒泡
- 从时间复杂度优势上 插入 = 冒泡 > 选择
- 从稳定性上 插入 = 冒泡 > 选择
欢迎有不理解的朋友向我提问。