# 【数据结构】平衡二叉树 (AVL 树) 怎么实现平衡
本篇采用 JAVA 语言简述
# 简述
AVL 是一种能自我调节的平衡二叉树,它相比与普通二叉树新增,删除操作复杂,但可以避免一些极端情况。
# AVL 树是如何保持平衡的
是通过旋转保持左右节点的平衡,一共有四种旋转方式,根据不同的插入使用不同的旋转方法。
词义解释:上根 (自己造的为了方便本文理解还请见谅,也可以叫父根),左子树,右子树,新节点。意思如下图
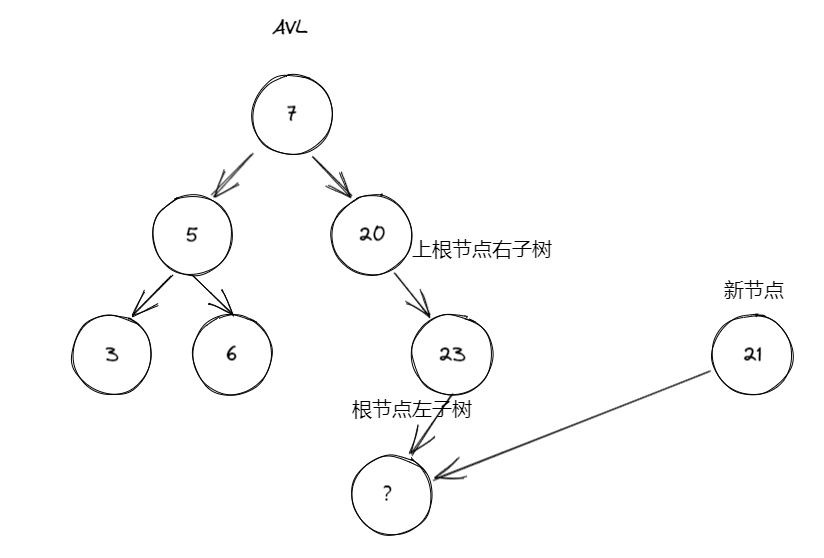
| 插入方式 | 描述 | 旋转方式 | 旋转核心 |
|---|---|---|---|
| LL | 在上根的左子树根节点的左子树上插入节点而破坏平衡 | 右旋转 | 不平衡的节点 |
| RR | 在上根的右子树根节点的右子树上插入节点而破坏平衡 | 左旋转 | 不平衡的节点 |
| LR | 在上根的左子树根节点的右子树上插入节点而破坏平衡 | 先左旋后右旋 | 不平衡节点下左树节点、不平衡的节点 |
| RL | 在上根的右子树根节点的左子树上插入节点而破坏平衡 | 先右旋后左旋 | 不平衡节点下右树节点、不平衡的节点 |
快速记忆:插入方式的命名 L 是 Left (左) 的首字母,R 是 Right (右),它们意思相反,插入方式的第一个字母是上根节点的左右,第二个形容的是数据最后放在根节点的左右。如果第一个字母和第一个字符相同,则旋转方式为字母相反意思,如果第一个字母和第一个字母不相同,旋转方式为两次,且顺序为字母顺序。
# 节点介绍
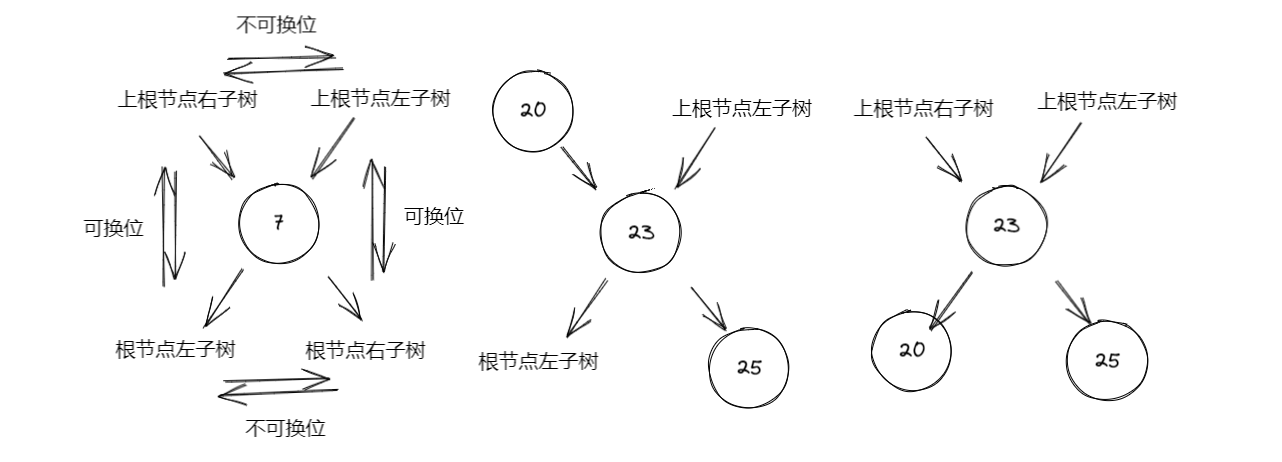
每个节点有四种情况,如上图所示,20 从 23 的上根节点右树点变为 23 的根节点左树如同时钟的逆时针旋转也叫左旋转,所以顺时针旋转叫右旋转。虽然看起来只有一个节点改变了位置,但高度却降低了,看起来很像旋转。如下
# 什么时候用左旋转,右旋转
判断条件思路如下
- 在发现一个节点的两边子树不平衡的时候要用旋转
- 在第一个条件下比较两个高度不平衡子树高度,高的一方子节点是旋转节点,不平衡的是中心节点,旋转节点在中心节点左边就是右旋转,在中心节点右边就是左旋转 (需要等三个条件执行完)
- 在第二个条件基础上知道旋转节点是左右哪个节点后,再对这个节点下方的左右树做一次高度比较,如果这个旋转节点是上根的左边,则旋转节点下右树比左树高或者相等下需要加一次左旋转,如果这个节点在上根的右边,则旋转节点下左树比右树高或者相等下需要加一次右旋转。( 这段比较难理解,加的这次旋转是为了让某一边比另一边高 2,然后再经过条件而的旋转,再次一加一减平衡,可看下图,删除 100 节点)

# 一个旋转中心节点,一个要旋转的节点
当某个节点发现左树和右树高度相差为 2 的时候,这表明节点下方的数据就不平衡,先判断那边树高,再将新入数与高树节点值进行对比判断是该节点的左树还是右树 (这种思路原理还是比较两树高,详情原因请参考前文旋转),再根据前表格写的方向决定旋转方向和次数。最多两个旋转中心点。要旋转的节点一定是中心点下左右两边最高的那棵树。

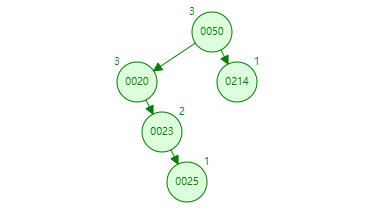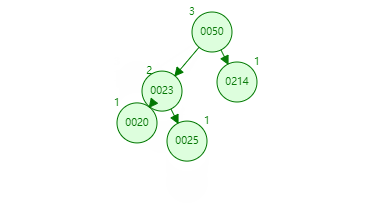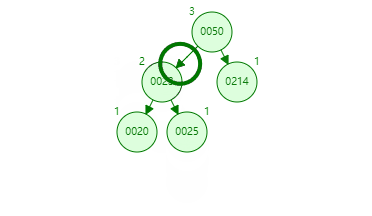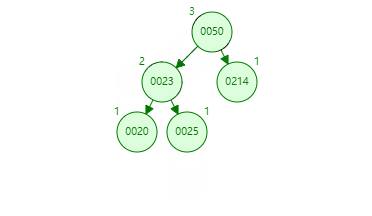
就拿上面举例,发现左右树高度相差为 2 的是 20 节点,在比较左右树,发现右树高,再比较右树的 23 和要入的新值 25,知道 25 在 23 节点的右树下,得到右 - 右,也就是 RR,所以使用左旋转,中心点就是 20,要旋转的点就是 23。
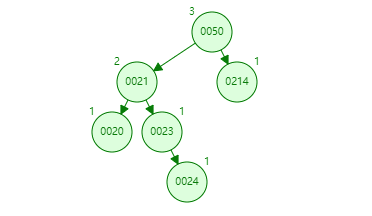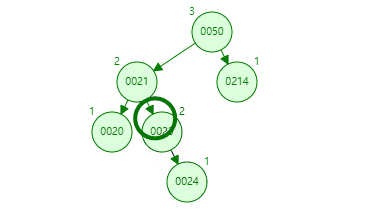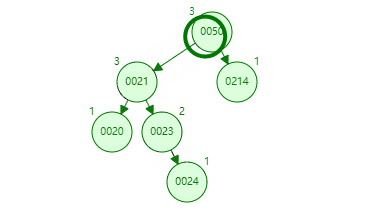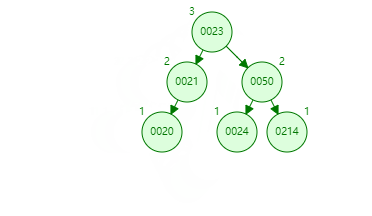
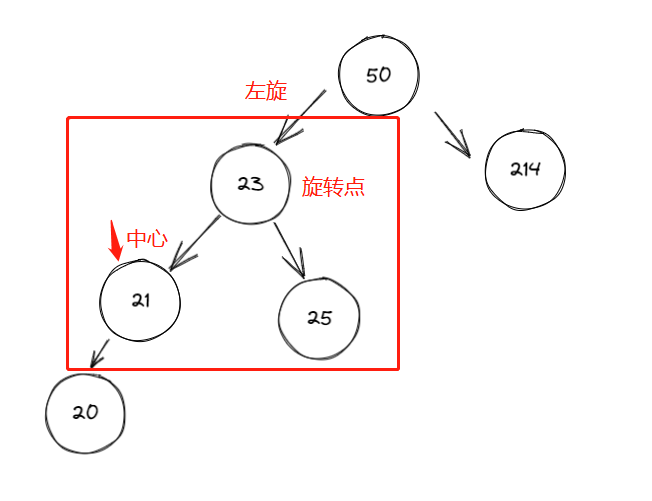
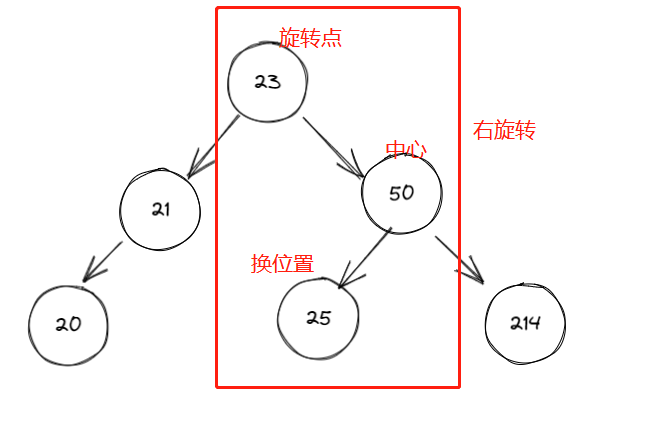
再看一个例子,首先发现左右高度相差为 2 的是 50 节点,在比较左右树,发现左树高,再比较左树的 21 和要入的新值 24,知道 24 在 21 节点的右下,得左 - 右,也就是 LR,所以第一次左旋转,中心点是 21,因为不平衡节点的左树最高,旋转的节点是 23,因为它高。第二次是中心点 50,旋转点是 23。这图中间状态如下。
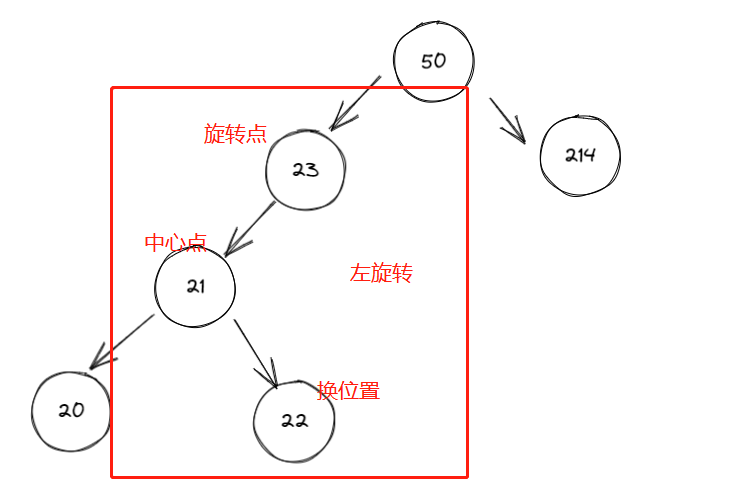
# 换位置
通过上面第二个例子,我们可以看到一个这里使用了一个基本的原则,中心节点比旋转节点大,那么旋转节点下的左右树所有子节点都比中心节点小,都可以挂在中心节点的左边。反过来也就是中心节点比旋转节点小,那么旋转节点下的左右树所有子节点都比中心节点大,都可以挂在另一个节点的右边,这就是第一次左旋转时也用到,只是 23 节点的左树没有,如果插入的是 22 就可以看出来。
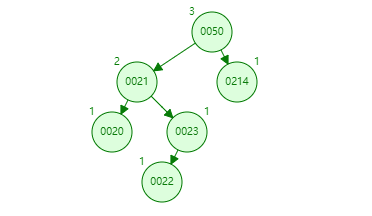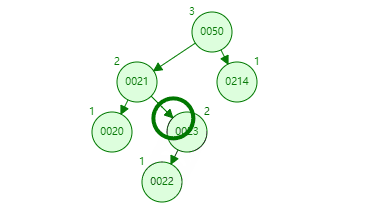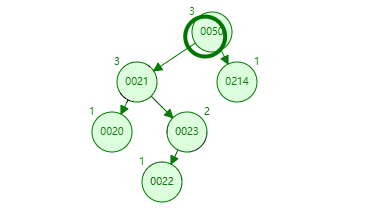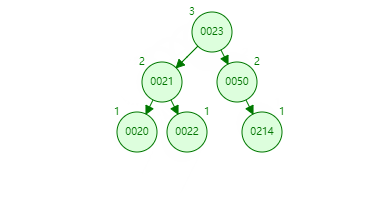
这里简单分析下,还是首先发现左右高度相差为 2 的是 50 节点,在比较左右树,发现左树高,再比较左树的 21 和要入的新值 22,知道 22 在 21 节点的右下,得左 - 右,也就是 LR。第一次左旋转时图如下
# 删除节点
删除节点如何保持 AVL 树的平衡,删除节点的思路,还是替换,不是节点下左右子树竞争一下谁上来。替换用的就是一个原则就是左子树下的最大值也比右子树最小值小。被替换的是删除的值,替换的值根据原则有两个选项,一个是删除值节点下左树最大值,一个是删除节点下右树最小值。下图替换用的是删除值节点下左树最大值。(删除 22)
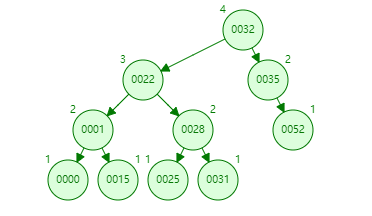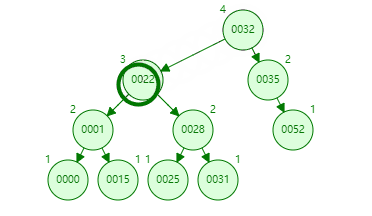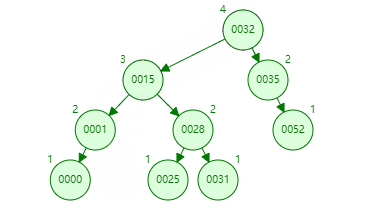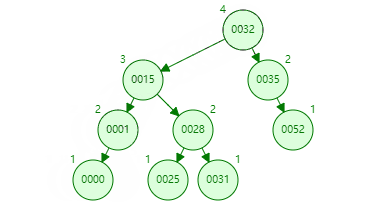
最后再从最小值递归向上检查是否有发现平衡被破坏的节点,再进行相应的旋转。把最小值抛弃掉。
# 实现思路总结
根据前文分析,可抓住几个要点,从而实现 AVL 的增删查
- 每个节点至少三个属性分布是一个左树箭头,和一个右树箭头,与一个当前层次数
- 不论增还是删,都需要向上递归直至找到发现不平横点,然后判断对其影响是 RR,LL,RL,LR 中的哪一种,再换位置实现旋转
- 左子树下的最大值也比右子树最小值小 (不然怎么到左子树去了)
# 节点类
private static class AVLNode<E> { | |
E element; | |
AVLNode<E> left; // 左树 | |
AVLNode<E> right;// 右树 | |
int height; // 树高度 | |
public AVLNode(E element) { | |
this(element, null, null); | |
} | |
public AVLNode(E element, AVLNode<E> left, AVLNode<E> right) { | |
this.element = element; | |
this.left = left; | |
this.right = right; | |
} | |
} |
# 左旋转代码实现
/** | |
* 获取指定树的高度 | |
*/ | |
private int height(AVLNode<E> t) { | |
return t == null ? -1 : t.height; | |
} | |
//t 中心,newTree 旋转节点 | |
private AVLNode<E> leftRotate(AVLNode t) { | |
AVLNode<E> newTree = t.right; // 取出要旋转点节点 | |
t.right = newTree.left; // 将旋转的节点左树给中心节点的右树 (换位置) | |
newTree.left = t; // 将旋转的节点左树指向旋转中心 (左旋转) | |
t.height = Math.max(height(t.left), height(t.right)) + 1; // 比较左右两树高,取最高 + 1,更新层级 | |
newTree.height = Math.max(height(newTree.left), height(newTree.right)) + 1; // 比较左右两树高,取最高 + 1 | |
return newTree; // 返回旋转节点 | |
} |
# 右旋转代码实现
//t 中心,newTree 旋转节点 | |
private AVLNode<E> rightRotate(AVLNode<E> t) { | |
AVLNode newTree = t.left; // 取出要旋转点节点 | |
t.left = newTree.right; // 将旋转的节点右树给中心节点的左树 (换位置) | |
newTree.right = t; // 将旋转的节点右树指向旋转中心 (右旋转) | |
t.height = Math.max(height(t.left), height(t.right)) + 1;// 比较左右两树高,取最高 + 1,更新层级 | |
newTree.height = Math.max(height(newTree.left), height(newTree.right)) + 1;// 比较左右两树高,取最高 + 1 | |
return newTree;// 返回旋转节点 | |
} |
# 新增节点
public AVLNode<E> insert(E x, AVLNode<E> t) { | |
if (t == null) { | |
return new AVLNode<E>(x); | |
} | |
// 先比较 是插当前节点的左边还是插右边 | |
int compareResult = x.compareTo(t.element); | |
if (compareResult < 0) {// 插到左子树上,若该节点发现不平衡,则一定是左树高于右树 所以是 L | |
t.left = insert(x, t.left); | |
// 插入之后要判断是否打破了平衡,因为插入的是左子树,只有左子树才会打破平衡,用左子树的高减去右子树的高 | |
if (height(t.left) - height(t.right) == 2) { | |
// 如果等于 2,说明平衡被打破了,这里比较的是插入值在这个节点的左子树 (L) 右子树 (R). | |
if (x.compareTo(t.left.element) < 0) { | |
// 如果 x 小于 t 的左子树的值,那么 x 会被插到 t 的左子树的左子树上,符合 LL 用右旋转调整。 | |
t = rightRotate(t); | |
} else { | |
// 如果 x 大于 t 的左子树的值,则会被插到 t 的左子树的右子树上,符合 LR,用先左旋转后右旋转来矫正。 | |
t.left = leftRotate(t.left); // 发现不平衡节点的左节点为中心,因为插入的是左树,它比右树高,先左旋转 | |
t = rightRotate(t);// 发现不平衡节点为中心,右旋转 | |
} | |
} | |
} else if (compareResult > 0) {// 插到右子树上,若该节点发现不平衡,则一定是右树高于左树 所以是 R | |
t.right = insert(x, t.right); // 向下递归插入 | |
// 插入之后要判断是否打破了平衡,因为插入的是右子树,只有右子树才会打破平衡,用右子树的高减去左子树的高 | |
if (height(t.right) - height(t.left) == 2) { | |
// 如果等于 2,说明平衡被打破了 | |
if (x.compareTo(t.right.element) > 0) { //x 大于 t 的右子树的值,那么 x 会被插到 t 的右子树的右子树 (R) | |
// 符合 RR 用左旋转调整 | |
t = leftRotate(t); | |
} else { //x 小于 t 的右子树的值,那么 x 会被插到 t 的右子树的左子树 (L) | |
// 符合 RL 先用右旋转调整再用左旋转 | |
t.right = rightRotate(t.right); // 发现不平衡节点的右节点为中心,因为插入的是右树,它比左树高,先右旋转 | |
t = leftRotate(t); // 发现不平衡节点为中心,左旋转 | |
} | |
} | |
} else { | |
// 已经有这个值了 | |
} | |
t.height = Math.max(height(t.left), height(t.right)) + 1; | |
return t; | |
} |
# 删除节点
根据上一章节所说删除一个节点的原理,根据这个原理去删除,思路应该是
- 递归查下,找到要删除的节点
- 若该节点没有左树或者右树,则将树直接上,并退出递归,判断左右树是否失去平衡
- 若左树右树都有,则在当前层,递归找到该节点其右子树的最小数据代替该节点的数据,并再次递归删除最小数据
- 直到递归找到要删除的最小节点,该节点下肯定没有最小值左树,回到第二个条件。
private AVLNode<E> remove(E x, AVLNode<E> t) { | |
if (t == null) | |
return null; | |
int compareResult = x.compareTo(t.element); | |
if (compareResult < 0) { // 要删除的元素在该节点左树上,若该节点发现不平衡,则一定是右树高于左树 所以是 R | |
t.left = remove(x, t.left); // 从左树递归,返回一定是一个在递归中平衡好的树 | |
// 因为最开始一定是平衡的,现在左树发生了减少,所以左子树高度最大可能高度降 1,也就是左子树比右子树高度少 1 的时候,这个节点可能不平衡,左子树高度可能比右子树高度最少小 2 了 | |
// 只有右子树才会打破平衡,用右子树的高减去左子树的高 | |
if (height(t.right) - height(t.left) == 2) { | |
// 如果等于 2,说明平衡被打破了,但删除无法像新增一样,通过要删除的值判断右节点怎么转保持平衡,这里判断的奥秘是该节点下的左右树谁高 | |
if (height(t.right.left) < height(t.right.right)) { // R | |
// 符合 RR 用左旋转调整 | |
t = leftRotate(t); | |
} else { // L | |
// 符合 RL 先用右旋转调整再用左旋转 | |
t.right = rightRotate(t.right); // 发现不平衡节点的右节点为中心,因为该中心节点左树存在,所以先右旋转 (原理参考前文) | |
t = leftRotate(t); // 发现不平衡节点为中心,左旋转 | |
} | |
} | |
// 完了之后更新 height 值 | |
t.height = Math.max(height(t.left), height(t.right)) + 1; | |
} else if (compareResult > 0) { // 要删除的元素在该节点右树上,若该节点发现不平衡,则一定是左树高于右树 所以是 L | |
t.right = remove(x, t.right); // 从右树递归,返回一定是一个在递归中平衡好的树 | |
// 只有左子树才会打破平衡,用左子树的高减去右子树的高 | |
if (height(t.left) - height(t.right) == 2) { | |
// 如果等于 2,说明平衡被打破了,但删除无法像新增一样,通过要删除的值判断左节点怎么转保持平衡,这里判断的奥秘是该节点左子树的右节点是否存在。 | |
if (height(t.left.left) > height(t.left.right)){ // 不存在就是 L | |
// 符合 LL 用右旋转调整 | |
t = rightRotate(t); | |
} else { // R | |
// 符合 LR 先用左旋转调整再用右旋转 | |
t.left = leftRotate(t.left); // 发现不平衡节点的左节点为中心,因为该中心节点右树存在,所以先左旋转 (原理参考前文) | |
t = rightRotate(t); // 发现不平衡节点为中心,右旋转 | |
} | |
} | |
// 完了之后更新 height 值 | |
t.height = Math.max(height(t.left), height(t.right)) + 1; | |
} else if (t.left != null && t.right != null) { // 要删除的元素就是这个节点,但该节点下有左右树,且平衡 | |
// 默认用其右子树的最小数据代替该节点的数据并递归的删除那个节点 | |
AVLNode<E> min = t.right; // 先取右子树 | |
while (min.left != null) { // 递归获取左数最小值 | |
min = min.left; | |
} | |
t.element = min.element; // 当前节点替换为最小值 | |
t.right = remove(t.element, t.right); // 第二次递归删除,这次删除的是查出来的这个最小值 | |
t = balanceChild(t); // 判断是否平衡 | |
// 完了之后更新 height 值 | |
t.height = Math.max(height(t.left), height(t.right)) + 1; | |
} else { | |
// 要删除的元素就是这个节点 ,但左右树不全在,所以返回尽可能存在的一边树,该树节点下方无影响所以肯定是平衡的 | |
t = (t.left != null) ? t.left : t.right; | |
} | |
return t; // 返回一个已平衡的 AVL 树 | |
} |
# 总结
待续,并发问题